Rekurentné neurónové siete
Ak chceme po napísaní slova vo vete predpovedať, aké ďalšie slovo bude v tejto vete nasledovať, potrebujeme zobrať do úvahy predchádzajúce slová. Musíme si teda nejakým spôsobom pamätať históriu. Bežné dopredné neurónové siete však takéto niečo neumožňujú. Spracuvávajú všetky vstupy len ako navzájom nezávislé a nevedia teda do výstupu nijako premietnuť žiadne informácie z doterajších predchádzajúcich vstupov. Na takéto a podobné problémy však vieme použiť rekurentné neurónové siete (stretnete sa aj so skratkou RNN). Ich aplikácie nájdeme okrem spracovania textu a reči aj v analýze obrazu či rozpoznávaní hlasu.
Hlavný rozdiel oproti klasickým dopredným sieťam je v tom, že rekurentné siete povoľujú vo svojej architektúre cykly, ako je uvedené nižšie.
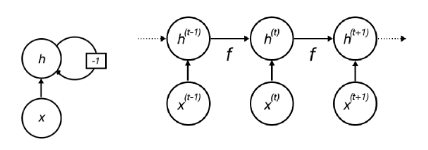
Neurón rekurentnej siete a zmena jeho stavu v čase, zdroj: vlastné
Typy rekurentných sietí
Rekurentné neurónové siete môžu mať nespočetné množstvo rôznych architektúr, napríklad:
- Rekurentná sieť s výstupom v každom čase a spätným prepojením skrytých jednotiek.
- Rekurentná sieť s výstupom v každom čase, kde výstup siete je prepojený so skrytými jednotkami.
- Rekurentná sieť, ktorá má prepojenia medzi skrytými jednotkami, spracuje kompletnú sekvenciu a produkuje len jednu výstupnú hodnotu.
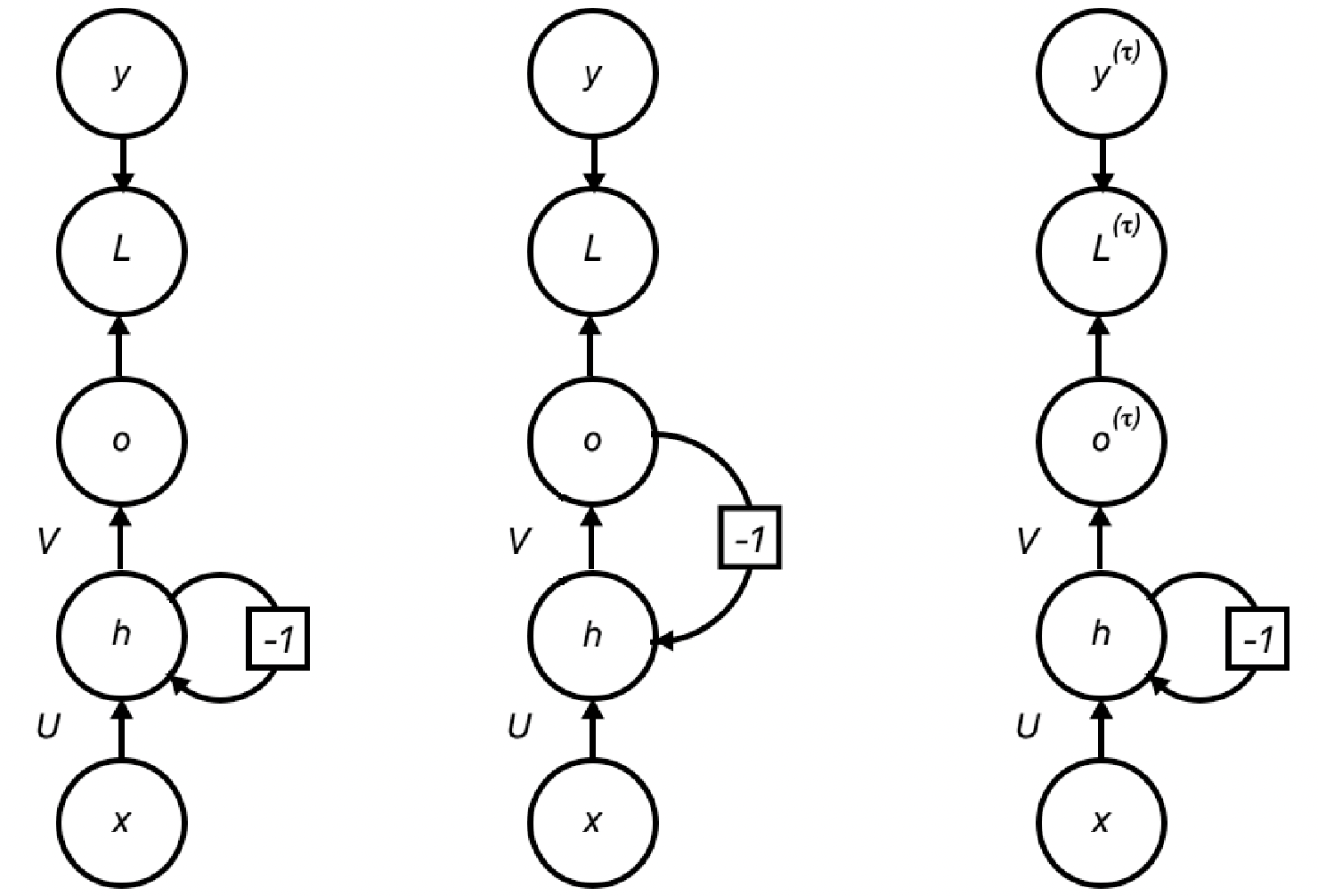
Rôzne typy rekurentných neurónových sietí zdroj: vlastné
Zoberme si prvú zo spomenutých architektúr a vytvoríme rovnice pre dopredné šírenie. Zameriame sa na úlohu predikovania nasledujúceho slova. Pre tento prípad si definujeme aktivačné funkcie, ktoré sú potrebné na sformulovanie siete. Ako aktivačnú funkciu skrytej vrstvy použijeme tangens hyperbolický a ako výstupná funkcia bude použitý softmax, ktorý reprezentuje pravdepodobnosť i predikcie jednotlivých slov. Teraz môžeme definovať dopredné šírenie našej rekurentnej siete ako:
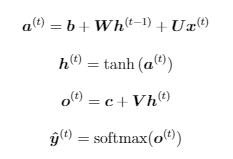
kde b a c sú vektory biasov a W, U a V sú jednotlivé matice váh. Takýto druh rekurentnej siete mapuje vstupnú sekvenciu do výstupnej o rovnakej veľkosti. Celková chyba takejto siete je len suma čiastkových chýb v jednotlivých časoch. Ako príklad môžeme uviesť log-pravedepodobnostnú chybovú funkciu: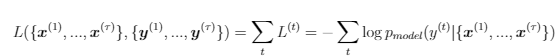
Ďalšie architektúry neurónových sietí
Vypočítanie gradientu takejto chybovej funkcie je náročná operácia. Na jeho vypočítanie potrebujeme vypočítať dopredné šírenie a následne spätné. Zložitosť je o(τ) a proces nemôže byť paralelizovaný, pretože výpočet je sekvenčný. Inak povedané, každý stav môžeme vypočítať až po tom, ako je vypočítaný jeho predchádzajúci. Každý zo stavov musí byť uložený, pokiaľ neprejde spätné šírenie a z tohto dôvodu môžeme rovnako povedať, že tento proces je náročný aj na pamäť. Tento algoritmus trénovania sa nazýva Algoritmus spätného šírenia chyby vzhľadom na čas (z ang.Back-propagation through time, BPTT), pri ktorej však nastáva tzv. problém miznúceho gradientu. Vzniká kvôli tomu, že sieť sa musí pri učení dlhých časových závislostí pozerať ďaleko do minulosti. To však spôsobuje, že gradienty pri učení konvergujú k hodnote 0, čiže vôbec nedochádza k úprave váh a sieť sa tak netrénuje.
Z tohto dôvodu boli navrhnuté koncepty, ktoré sa snažia problém miznúceho gradientu odstrániť. Najznámejšie z nich sú Long Short Term Memory (LSTM, 1997) a Gated Recurrent Units (GRU, 2014), ktoré si predstavíme v ďalšom pokračovaní.




