Náhľad do algoritmu rozhodovací strom
Úvodný obrázok zdroj: Arek Socha, Pixabay
Rozhodovacie stromy patria medzi široko používané metódy strojového učenia, ktoré nachádzajú svoje uplatnenie rovnako v úlohách klasifikácie ako aj regresie. V princípe ide o hierarchický, viacstupňový binárny rozhodovací systém, v ktorom sa postupne vyhodnocuje splnenie/nesplnenie (if/else) rozhodovacích kritérií alebo podmienok, pokiaľ sa nedostaneme k akceptovanej triede alebo riešeniu.
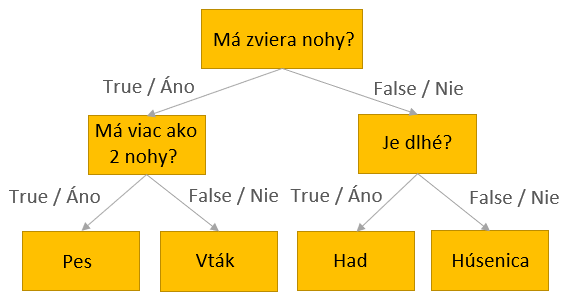
Rozhodovací strom, zdroj: vlastné
V procese rozhodovania sa postupuje od koreňa stromu postupne cez jednotlivé uzly, ktoré vytvárajú vetve stromu s listami. Napriek tomu, že existuje viacero rozličných druhov rozhodovacích stromov, vytváranie stromových štruktúr sa zväčša riadi tým, že rozhodovacie kritéria v jednotlivých uzloch sú zoradené podľa informačnej dôležitosti. Príznak alebo kritérium, ktorý má najväčšiu váhu a umožňuje najlepšie separovať vstupné dáta do 2 binárnych tried (áno/nie) sa stáva koreňom stromu. Ďalšie uzly sú postupne tvorené zostávajúcimi kritériami s menšou váhou, pričom každý uzol vytvára dvoch binárnych potomkov. V procese rozhodovania sa postupuje po jednotlivých vetvách stromu, až sa dostaneme k hľadanej triede alebo riešeniu (list).
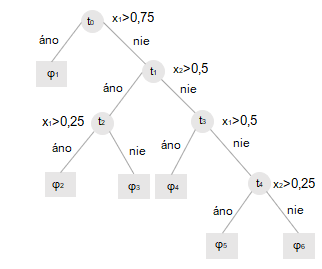Ukážka OBDT, zdroj: vlastné
Štandardný binárny rozhodovací strom
Obrázok hore zobrazuje tzv. štandardný binárny rozhodovací strom (ordinary binary classification tree OBDT), v ktorom sa sekvenčne vyhodnocuje podmienka, či je daný príznak xi <= a . Takýto typ rozhodovacieho stromu rozdeľuje príznakový priestor na hyper-obdĺžniky, ktorých strany sú paralelné s osami súradnicového systému (viď obr. nižšie).
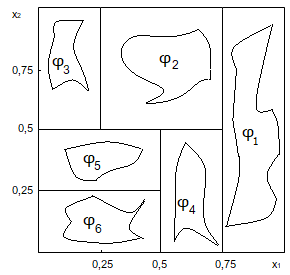Ukážka hyper-obdĺžnikov OBDT, zdroj:vlastné
Najčastejšie používaným algoritmom, ktorý využíva princíp rozhodovacích stromov, je algoritmus ID3 (príp. jeho rozšírená verzia C4.5). Tento algoritmus využíva ako mieru dôležitosti jednotlivých príznakov alebo kritérií, ktoré tvoria vetvy stromu, entropiu a tzv. informačný zisk. Entropia popisuje množstvo informácie obsiahnutej v danom príznaku alebo kritériu a informačný zisk sleduje zmeny entropie pri použití konkrétneho príznaku. Matematicky to možno popísať nasledovne, :
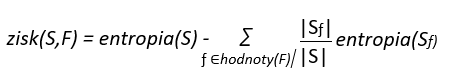
kde S je množina príkladov, F je množina možných príznakov v množine S , |Sf| je počet príkladov, ktoré majú hodnotu príznaku f a |S| je celkový počet príkladov. Pre celú množinu príznakov sa teda vypočíta informačný zisk a príznak s najväčšou hodnotou zisku sa stáva koreňom stromu. Pre zostávajúce príznaky sa prepočíta informačný zisk a opäť sa vyberie príznak s najvyššou hodnotou a vytvorí uzol stromu – takto sa postupuje iteratívne, až kým nie je vyčerpaná celá množina možných príznakov. Výsledkom je vygenerovaný model – rozhodovací strom. Kritickým faktorom je veľkosť stromu a je potrebné zabezpečiť, aby nebol ani príliš veľký, ani príliš malý. V prípade veľkých stromov je potrebné vykonávať tzv. prerezávanie stromu (angl. prunning). Medzi výhody rozhodovacích stromov patrí úplná invariancia algoritmov voči škálovaniu dát, rovnako ako aj ľahká zrozumiteľnosť a vizualizácia vytvorených modelov. Spomedzi nevýhod týchto algoritmov možno spomenúť tendenciu k pre-trénovaniu a ich nízku schopnosť generalizácie.
