Učiace metódy založené na Bayesovej teórii rozhodovania
Úvodný obrázok zdroj: Wikimedia Commons – upravené
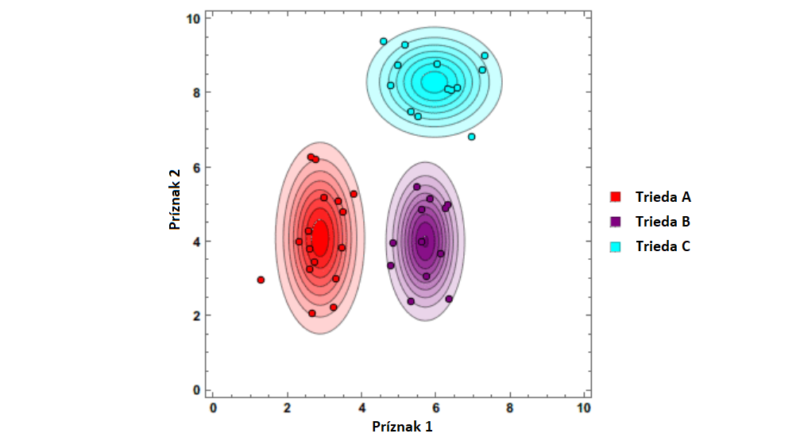
V mnohých úlohách, s ktorými sa stretáva umelá inteligencia a strojové učenie, sa na reprezentáciu dát používajú skupiny príznakov, ktoré majú určitú štatistickú povahu. Rozhodovanie o príslušnosti dát k určitej triede sa deje na základe pravdepodobnostných vlastností. Jedným z možných prístupov, ako možno modelovať takéto pravdepodobnostné vlastnosti, je Bayesov teorém, ktorý slúži ako základný kameň pre celú skupinu učiacich metód nazývaných spoločne ako bayesovské učenie.
Okrem typických predstaviteľov ako sú naivný Bayesov klasifikátor či bayesovské učenie s odmenou, nachádza toto učenie uplatnenie v rôznych neurónových sieťach a špeciálny význam má v Markovových reťazcoch. Bayesovské učenie patrí do kategórie generatívnych modelov, ktoré umožňuje na základe znalostí skrytého rozdelenia pravdepodobnosti trénovacích dát zostavenie štatistického modelu. Tento model dokáže dáta nielen priradiť k určitej triede a poskytnúť nám odhad, s akou pravdepodobnosťou je naša klasifikácia správna, ale dokáže vytvárať úplne nové dáta s rovnakými štatistickými vlastnosťami, aké majú trénovacie dáta.
Bayesov teorém
Autor teorému, britský štatistik, filozof a teológ Thomas Bayes, vo svojom diele skvele opísal podmienenú pravdepodobnosť určitej udalosti na základe predchádzajúcej znalosti podmienok, ktoré by mohli viesť k danej udalosti. Stručne sa dá táto veta, známa aj ako Bayesova inferencia, popísať takto. Ak máme 2 náhodné udalosti w a z so známymi pravdepodobnosťami P(w) a P(z), potom pre podmienenú pravdepodobnosť P(z|w) udalosti z za predpokladu, že došlo k udalosti w, platí nasledovné:
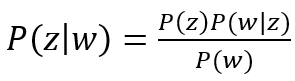 ,
,
kde P(w|z) označuje pravdepodobnosť udalosti w za podmienky, že nastane udalosť z. Pre väčšiu názornosť si uveďme takýto príklad.
Filmová databáza obsahuje krátke textové hodnotenia divákov a celkový dojem z filmu – pozitívny resp. negatívny. 15 % filmov je celkovo hodnotená negatívne. 80 % pozitívnych hodnotení zahŕňa v popise slovo „super“. 8 % negatívnych hodnotení tiež obsahuje toto slovo. Aká je pravdepodobnosť, že nové hodnotenie bude negatívne, ak obsahuje slovo „super“? Uvažujme vzorku 1000 respondentov-hodnotení. Pred analýzou textového hodnotenia divákov dostávame:
skupina X: 150 negatívnych hodnotení
skupina Y: 850 pozitívnych hodnotení
Na základe textov divákov môžeme vytvoriť nasledovné skupiny:
skupina 1: 680 pozitívnych hodnotení so slovom „super“ (850 * 0,8)
skupina 2: 170 pozitívnych hodnotení bez slova „super“
skupina 3: 12 negatívnych hodnotení so slovom „super“ (150 * 0,08)
skupina 4: 138 negatívnych hodnotení bez slova „super“
Túto situáciu ilustruje obrázok nižšie.
Výsledná podmienená pravdepodobnosť je teda 12/(12+680) = 1,73 %.
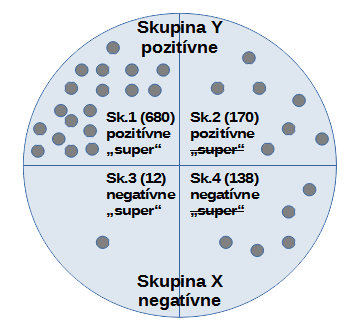
Zdroj: vlastné
V „bayesovskom svete“ môžeme vyššie uvedenú rovnicu prepísať do nasledovnej podoby (označenie je uvedené v pôvodnom anglickom jazyku pre lepšiu zrozumiteľnosť):
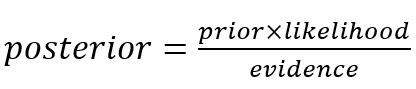
Posterior označuje aposteriórnu pravdepodobnosť alebo hypotézu, ktorú chceme preskúmať (Je hodnotenie negatívne, ak obsahuje slovo „super“?). Prior pomenúva apriórnu pravdepodobnosť a zodpovedá úvodnej znalosti (aké časté je negatívne hodnotenie filmu) – tiež sa zvykne volať stupeň viery v udalosť z. Likelihood popisuje pravdepodobnosť udalosti w pri predpoklade, že nastane udalosť z. Evidence označuje marginálnu pravdepodobnosť udalosti w. V praxi nás zaujíma len čitateľ výrazu, nakoľko menovateľ je nezávislý na skúmanej hypotéze, je teda konštantný a možno ho zanedbať.
Naivný Bayesov klasifikátor
Doteraz sme uvažovali len jednoduchý prípad s jednou náhodnou premennou (evidence). V konkrétnych reálnych úlohách sa však väčšinou stretávame s viacnásobnými premennými, takže miesto podmienenej pravdepodobnosti P(z|w) musíme počítať združenú pravdepodobnosť P(z|w1, w2, …, wn). Pre prípad s 2 náhodnými premennými platí nasledovný vzťah:
P(z|w1,w2) = P(w1|w2,z)P(w2|z)P(z)
pričom časť výrazu P(w1|w2, z) hovorí o tom, že podmienená pravdepodobnosť w1 závisí na w2 a zároveň aj na z, čo výrazne komplikuje výpočet a stáva sa ešte horším v prípade väčšieho počtu premenných. Pri predpoklade, že jednotlivé premenné sú medzi sebou nezávislé, môžeme zmiešané časti zanedbať a zjednodušiť P(w1|w2, z) na P(w1|z) a výraz teda možno prepísať ako
P(z|w1,w2) = P(w1|z)P(w2|z)P(z).
Tento prístup je síce trošku „naivný“, nakoľko v reálnom svete je tento prípad vzájomnej nezávislosti jednotlivých premenných skôr vzácny, avšak takto získal naivný Bayesov klasifikátor (NBC) svoje meno. Po vytvorení štatistického modelu sú na základe určitého rozhodovacieho pravidla dáta priradené k jednotlivým triedam. Bežným kandidátom je metóda MAP (Maximum a posteriori), ktorý vyberá danú triedu na základe najväčšej aposteriórnej pravdepodobnosti. NBC je v praxi široko využívaný, pretože v mnohých úlohách dokáže konkurovať alebo dokonca prekonať omnoho sofistikovanejšie metódy a poskytuje viacero výhodných vlastností ako sú napr. dostatočná presnosť predikcie dát, výpočtová výkonnosť, robustnosť a odolnosť voči chybným dátam či chýbajúcim hodnotám.