Úvod do neurónových sietí 2.časť

Úvodný obrázok zdroj: Gerd Altmann, Pixabay

Základnou jednotkou neurónovej siete je počítačový neurón. Tieto neuróny boli navrhnuté práve podľa neurónov v ľudskom mozgu. Neurón, ako taký, funguje v istej abstrakcii nasledovne. Cez vstupné zakončenia bunka prijme impulzy od susedných neurónov a zosumuje ich. Ak je výsledný súčet prijatých signálov väčší ako prahová hodnota, vyšle bunka signál ďalej ostatným neurónom cez svoje výstupné zakončenia. Množstvo signálu, ktoré je prenesené cez vstupné zakončenia neurónu je dané silou prepojenia (váhou), pričom tieto prepojenia môžu silnieť aj zoslabovať.

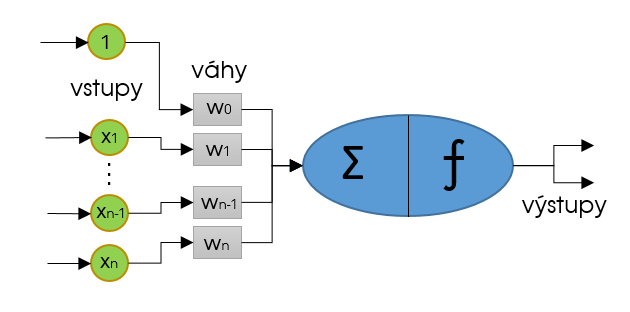Umelý počítačový neurón

Zdroj: vlastné

V počítačovej neurónovej sieti to funguje veľmi podobne. Prvý publikovaný typ počítačového neurónu, perceptron, funguje presne rovnako ako popísaný biologický neurón. Sčíta vstupy, resp. výstupy neurónov predchádzajúcej vrstvy x_i-1 , vynásobené silou prepojenia w_i-1 (váhami) a po porovnaní výsledku s prahovou hodnotou T vyšle ako svoj výstup hodnotu 0 alebo 1. Prahová hodnota T sa označuje ako bias jednotka b a je rovná b≡ -T. Matematicky je to vyjadrené nasledovne:

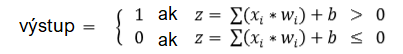
Pomocou tohto perceptronu je síce možné zostaviť funkčnú sieť, narazíme pri ňom ale na viacero nedostatkov. Zamyslime sa ešte raz, čo je podstatou strojového učenia. Máme známy vstup, známy výstup, ale nepoznáme funkciu y = F(x), ktorá pre tento vstup (x) vypočíta známy výstup (y). Pomocou strojového učenia sa snažíme nájsť aproximáciu G(x) tejto funkcie F(x), pričom táto funkcia v reálnych úlohách takmer nikdy nie je lineárna. Mnohé úlohy dokonca nie sú ani lineárne separovateľné (známy problém XOR), a tak použitie lineálnej funkcie nepripadá do úvahy. No ako ste si zrejme všimli, perceptron je práve lineárnou funkciou.

Na ďalší problém narazíme, keď sa budeme túto sieť snažiť natrénovať na konkrétnu úlohu. V stručnosti je trénovanie siete optimalizačná úloha, ktorá spočíva v upravení prepojení (váh) v sieti tak, aby sieť pri danom vstupe podala požadovaný výstup. Aktuálne sa na to používajú gradientové metódy, ktoré fungujú na princípe derivácií. Funkcia, ktorú používame na výpočet výstupu perceptronu je ale lineárna, a tak má na celom definičnom obore deriváciu rovnú 0, čiže takúto sieť nevieme týmto spôsobom vôbec trénovať.

Aktivačná funkcia

Riešenie ponúkajú iné typy neurónov. Napríklad sigmoid neurón, ktorého výstupom už nie je len celé číslo 0 alebo 1, ale reálne číslo z intervalu (0,1). To dosiahneme s použitím nelineárnej sigmoid funkcie:

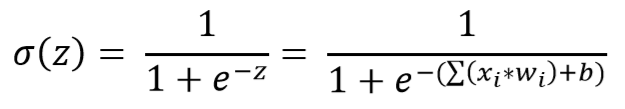
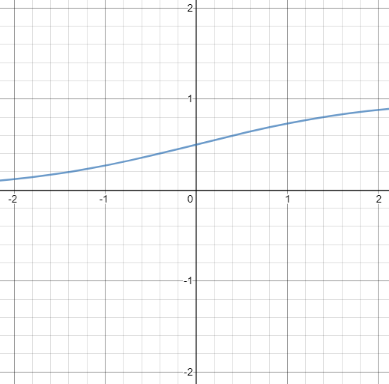
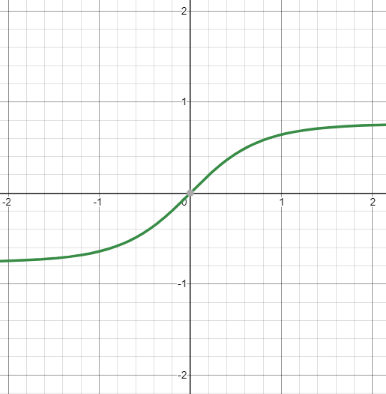
Funkciu σ(z) budeme označovať aktivačná funkcia f. Používajú sa však aj iné typy aktivačných funkcií, napríklad funkcia tanh (tangens hyperbolický). Má podobný priebeh ako sigmoid funkcia, rozdiel je však v tom, že jej výstupom je číslo z intervalu (-1, 1).

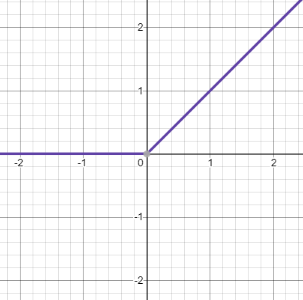
Veľmi často používanou je aj funkcia ReLU (Rectified Linear Unit), ktorú nájdeme hlavne v konvolučných neurónových sieťach. Jej predpis je R(z)=(0,z), takže záporné vstupy zmení na 0 a nezáporné hodnoty nechá bez zmeny, jej obor hodnôt je tak <0,∞>.

Forward propagation

Na nasledujúcom obrázku je príklad veľmi jednoduchej siete s jednou skrytou vrstvou. Ukážeme si na nej metódu „forward-propagation“, ktorá sa používa na prechod vstupných dát cez klasické dopredné siete. Vstupná vrstva tu má 2 neuróny, na vstupe je teda vektor  X=(x₁,x₂). Výstupná vrstva má len 1 neurón, výstupom je preto jedno číslo y. Sieť je doplnená o bias jednotky a ich prepojenia na nasledujúce vrstvy.

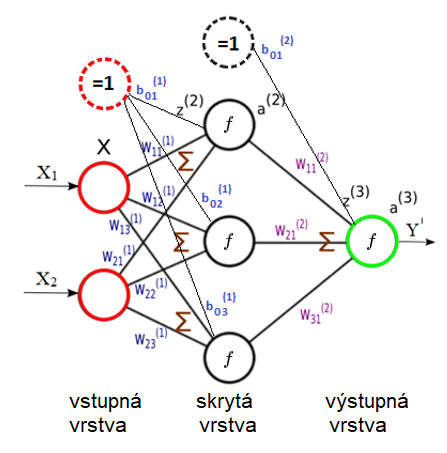
Forward propagation (upravené)

Ohodnotenia prepojení (váh) medzi vstupnou a skrytou vrstvou, vrátane váh pre bias jednotku sú uložené v matici o rozmeroch 3 x 3. Rozmer je podľa toho, že máme 2 normálne vstupy + 1 skrytá jednotka, a každý z týchto 3 vstupov je prepojený s 3 neurónmi v nasledujúcej vrstve:

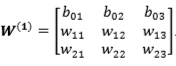
Namiesto toho, aby sme pre každý neurón skrytej vrstvy osobitne počítali hodnotu funkcie z, vypočítame hodnotu všetkých neurónov naraz maticovým vynásobením vektora vstupov X  a matice váh W⁽¹⁾, čím dostaneme vektor z⁽²⁾=(z₁ z₂ z₃), ktorý má 3 prvky, čo je rovné počtu neurónov v skrytej vrstve:

Na všetky prvky následne aplikujeme aktivačnú funkciu f, ktorou môže byť napríklad funkcia sigmoid. Dostaneme tak vektor a² = (a₁ a₂ a₃), ktorý je konečným výstupom skrytej vrstvy:

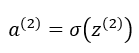
Rovnaký postup teraz zopakujeme medzi skrytou vrstvou a výstupnou, prípadne, ak by bolo v sieti viacero skrytých vrstiev, zopakujeme to aj medzi nimi. Opäť teda maticovo vynásobíme vstupy, resp. výstupy z predošlej vrstvy, vo vektore a²  a váhy medzi týmito vrstvami vo vektore W⁽²⁾=(b₀₁ w₁₁ w₂₁ w₃₁)^T. Všimnime si, že váhy už nie sú vo forme matice, ale vo forme vektora, pretože v nasledujúcej vrstve už je len 1 neurón, čiže máme akoby maticu 4×1, čo berieme ako vektor. Dostaneme teda hodnotu z⁽³⁾=a²*W⁽²⁾ , na ktoré opäť aplikujeme aktivačnú funkciu f a dostaneme konečný výstupný odhad a³=σ(z⁽³⁾)=y‘.

Zdroje: NN and DL

Ing. Juraj Muráň